Kasvun matematiikan perusteet ovat varmasti monelle tuttuja jo kouluajoilta. Kaikki ovat nähneet kasvukäyriä joko $TSLA:n, ÐOGE:n tai muun järkisijoituksen kurssissa unohtamatta tietenkään terveydenhuollossa käytettäviä pituutta seuraavia kasvukäyriä. Matemaattisen puhtaita ja kauniita nämä käyrät harvoin ovat, vaikka toisinaan jotain yksinkertaista matemaattista mallia kasvukäyrään tai sen osaan voikin soveltaa. Tässä jutussa esitellään järkkymättömällä asiantuntijuudella (5*5op suoritettu, kavereita Fyysikkokillasta) kasvun matematiikkaa.

Kasvua voi mallintaa matemaattisilla funktioilla. Peruskoulun matematiikasta, tai viimeistään phuksimatikoista kaikki varmasti muistavat, että funktio toimii kuin taikalaatikko, johon voi työntää numeron ja ottaa jonkun toisen numeron pois. Silloinhan tietyllä luvulla saa joka kerralla ulos saman luvun. Joskus on niin, että kun sisään menevä arvo kasvaa, niin myös ulos tuleva arvo on aina edellistä suurempi.

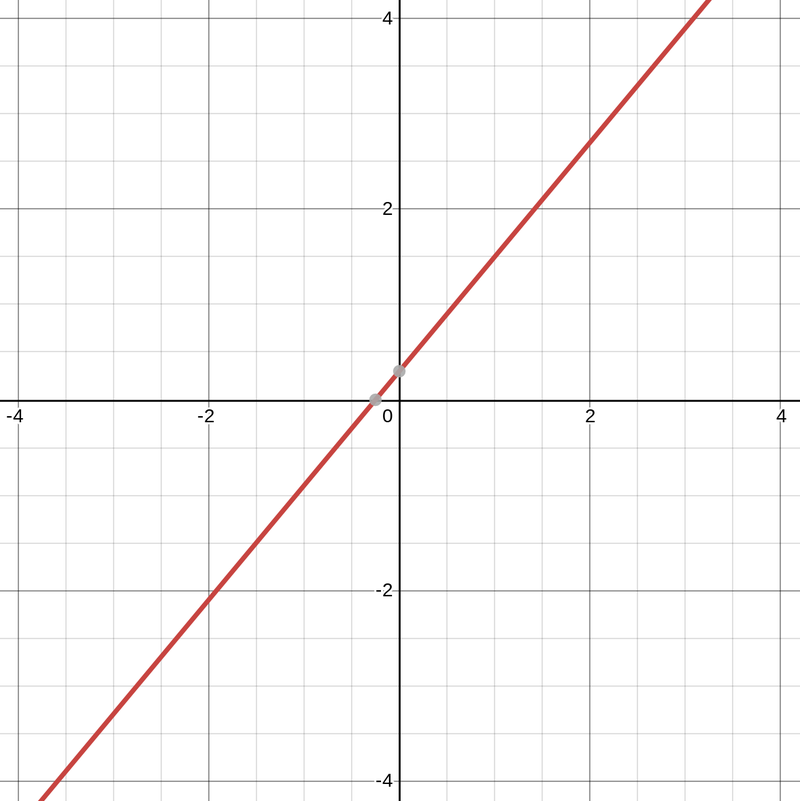
Kasvavia funktioita on lukuisia. Ehkäpä yksinkertaisin on suora. Kukapa meistä ei olisi joskus sovittanut suoraa mittaustuloksiin? Alla on funktion y = f(x) = 1,2x + 0.3 kuvaaja.

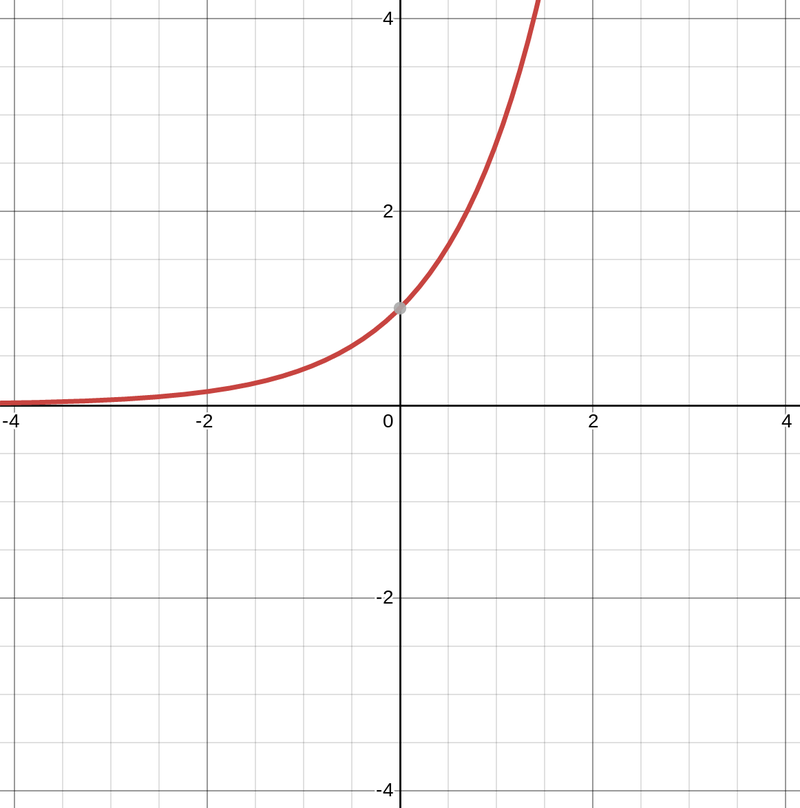
Eksponenttifunktio sopii ns. erittäin nopean kasvun kuvaamiseen. To the moon! e^x

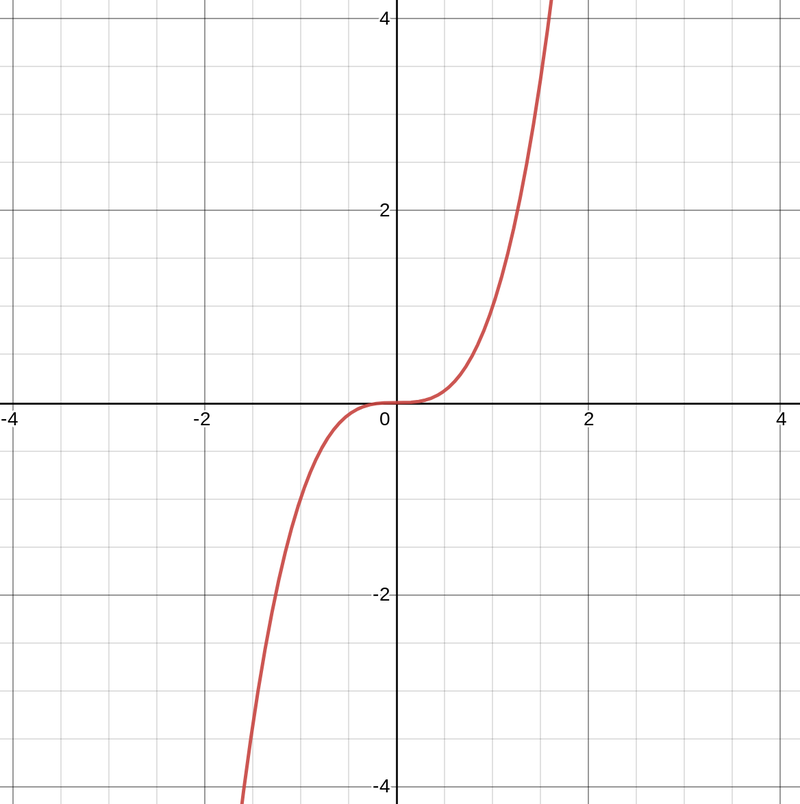
Jotain näiden väliltä tarjoavat esimerkiksi toisen ja kolmannen asteen funktiot sopivilla määrittelyjoukoilla. Alla on funktion f(x) = x^3 kuvaaja. Huomasitko muuten, että funktiolla on terassikohta, kun x = 0? Tämä on funktion derivaatan nollakohta, mutta kyseessä ei silti ole minimikohta (ei paikallinen eikä globaali). Kasvu siis pysähtyy, mutta jatkuu sitten taas.

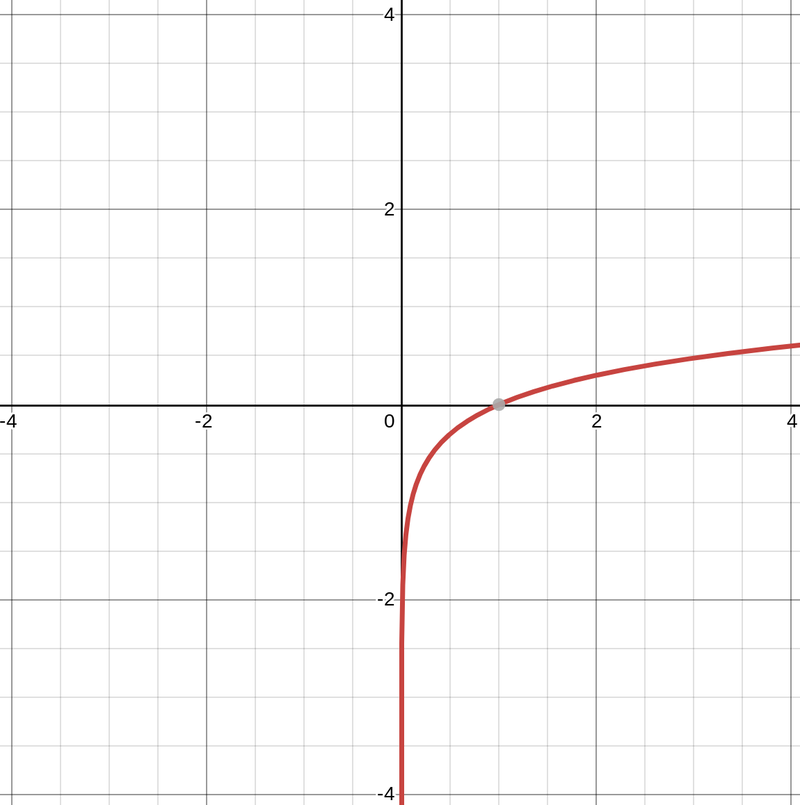
Logaritmista kasvua. y = log(x). Ei sovellu kryptointoilijoille, vaikka matka nollasta yhteen taittuukin reippaasti.

Mikä näistä on lempikasvufunktiosi, vai jäikö se uupumaan artikkelista? Kerro palautteesi fyssan kiltiksellä!